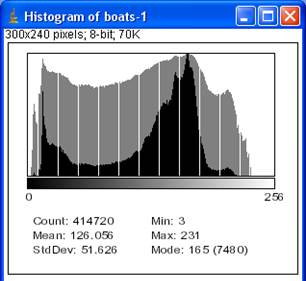Lösen Sie als Macro-Aufgabe: Laden Sie das Sample Image "Boats". Finden Sie heraus, wie man ein Histogramm H0 dieses Bildes erstellt und ermitteln Sie damit den höchsten Grauwert im Bild.

Erstellen Sie eine Kopie von "Boat" und spreizen Sie dort die Grauwertverteilung so, dass der höchste Grauwert 220 auf den Wert 231 kommt (2 Möglichkeiten)

Betrachten Sie das Histogramm H1 dieses neuen Bildes. Fällt Ihnen im Vergleich zu H0 etwas auf, und haben Sie eine Idee, wie man den Artefakt erklären kann?

Analog: Senken Sie den höchsten Grauwert um 5% ab.

Betrachten Sie das neue Histogramm H2. Fällt Ihnen etwas auf, und haben Sie eine Idee, wie man den (neuen) Artefakt erklären kann?

Wieviel Information steckt noch in dem Differenzbild "Original minus um 5% abgesenkte Kopie"? Spreizen Sie das Differenzbild wieder auf den vollen Grauwertbereich.

A.2. Aufgabe Binär-Merkmale

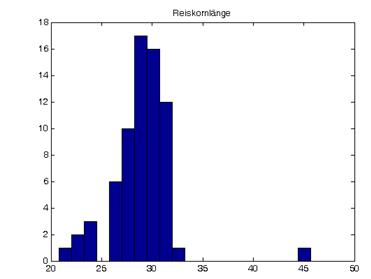
rice-morph-bin rice-hist-länge

Gegeben ein Binärbild rice-bin.png mit Reiskörnern. Implementieren Sie Algorithmen, die für alle ganz sichtbaren Reiskörner verschiedene Eigenschaften ermitteln

Anzahl
Größe (also Fläche = Area)
Bounding Box
Umfang (Perimeter)
Rundheit

Anleitung: Alle diese Eigenschaften können Sie über Befehle im Menu Analyze ermitteln. Machen Sie sich mit Set Measurements..., Analyze Particles... und Measure vertraut. Finden Sie heraus, wie man Ergebnisse im Results-Window erhält und speichern Sie die Ergebnisse in Results.xls. Nutzen Sie die Sortierfunktion von Excel, um Ausreisser in Größe und Breite Bounding Box zu finden, und lokalisieren Sie diese dann wieder um im Bild.

Aber wir wollen einige dieser Merkmale pro Reiskorn auch selbst nachrechnen.

Anleitung: Dazu wählen wir mit dem Wand Tool (Zauberstab) ein Reiskorn aus, erzeugen mit Edit – Selection – Create Mask ein neues Bild (die Maske Mask), das nur dieses Reiskorn enthält. Schreiben Sie nun ein Plugin, das auf Mask operiert und folgende Dinge ermittelt

die Projektion auf die x-Achse
die Projektion auf die y-Achse

Daraus können wir leicht berechnen und im Log-Window ausgeben:

die Fläche dieses Reiskorns
die Bounding Box dieses Reiskorns

mask

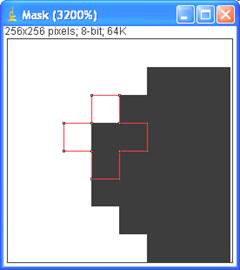
Nun zum Umfang: Ein vereinfachter Ansatz besteht darin, alle Pixel des Reiskorns zu zählen, die in ihrer 4er-Nachbarschaft mindestens ein Hintergrund-Pixel haben. Implementieren Sie dies im Plugin, und nehmen Sie die Anzahl dieser Pixel als Schätzwert für

den Umfang,
und – daraus abgeleitet – die Rundheit.

Vergleichen Sie die Ergebnisse Ihres Plugins für ein Reiskorn mit den entsprechenden Results von Analyze Particle... Stimmt's überein? – Bei Perimeter hat ImageJ einen nicht-ganzzahligen Wert (während unsere Näherung ganzzahlig ist). Können Sie erklären wieso?

A.3. Aufgabe Region Labeling

rice-morph-bin rice-label2rgb

Gegeben ein Binärbild rice-bin.png mit Reiskörnern. Damit der Computer die einzelnen, getrennten Regionen auch wirklich getrennt bearbeiten kann, müssen wir jedem Pixel einer Region einen eindeutigen Regions-Index zuweisen. Im Bild rechts hat jedes Reiskorn ein anderes Label 1,2,3,… und über eine Lookup-Table (LUT) wird jedem Reiskorn ein anderer Farbwert zugewiesen.

Implementieren Sie einen Algorithmus "Connected Region Labeling", der jede zusammenhängende weiße Region mit einem eindeutigen Index belegt.

Dabei soll der Algorithmus den Begriff "zusammenhängend" zunächst über 8er-Nachbarschaft umsetzen.

Schauen Sie sich dazu [Burger15, S. 228-232] an.

Empfehlung: Folgen Sie dem Pseudo-Code in [Burger15] bis zur Stelle „Kollision registrieren“. Aber anstatt die Kollisionen zu registrieren, reparieren Sie sie besser direkt an Ort und Stelle, das ist programmtechnisch einfacher: Wenn die kollidierenden Label {2,5} sind, dann ersetzen Sie im Bild jede 5 durch eine 2.

Zusatzaufgaben:

Durch die Kollisionsreparatur ergeben sich Gaps in den Label-Nummern. Schließen Sie diese Gaps, so dass am Ende aus dem höchsten Label-Wert (minus 1) die Anzahl der Regionen abgelesen werden kann.
Dokumentieren Sie Ihre Ergebnisse, indem Sie für jede gefundene Region im Result-Window ausgeben: Index, XStart, YStart, wobei (XStart,YStart) das erste Pixel jeder Region bei zeilenweisem Abscannen bezeichnet.
Vergleichen Sie Ihre Ergebnisse mit denen aus dem ImageJ-Befehl Analyze – Analyze Particles, indem Sie die Result-Listen vergleichen: Gleiche Anzahl von Regionen? Weitgehend gleiche Nummerierung?
Erweitern Sie das Plugin so, dass wahlweise auch über 4er-Nachbarschaft gearbeitet werden kann.

Literatur

[Burger15], Kap. 10.1.2, S. 228ff: Sequentielle Regionenmarkierung
[Umbaugh98], Kap. 2.6.2, S. 133f.
Image Processing Toolbox, Matlab-Help, Kapitel 9

A.4. Aufgabe Segmentierung

rice

Wir wollen im obigen Bild rice.png die Anzahl der Reiskörner zählen und die durchschnittliche Größe eines Reiskorns bestimmen.

Dazu muss man erstmal die Reiskörner erstmal vom Hintergrund abtrennen; diesen Prozess nennt man Segmentierung. Die Aufgabe ist gelöst, wenn wir ein Binärbild haben, in dem alle Reis-Pixel auf "1", alle Hintergrund-Pixel auf "0" stehen.

Wie segmentiert man das?

Anleitung: Überzeugen Sie sich, dass einfache Schwellwert-Binarisierung für keine Schwelle zum Erfolg führt. Eine Alternative wäre morphologische Segmentierung.

Laden Sie dazu von der ImageJ-Website https://imagej.nih.gov/ij/ das Plugin Grayscale Morphology, installieren es und machen sich mit seiner Wirkungsweise vertraut. Entwickeln Sie dann ein Macro, das die Segmentierungsaufgabe löst

Beim anschließenden Reiskörner-Zählen und Größe-Ermitteln ist wieder Analyze Particles... ein nützlicher Befehl (s.o.)

rice-perim

Zusatzaufgabe: Wie könnte eine morphologische Operation aussehen, mit der Sie den Outline aller Reiskörner (s. Bild) ermitteln können?

Literatur

· [Umbaugh98], Kap. 2.4.6

· [Burger05], Kap. 10 (insbes. S. 179ff.)

A.5. Histogramm-Ausgleich (Equalization)

copter2 copter2-equalized

Implementieren Sie ein Plugin, das den Histogramm-Ausgleich rechnet.

Stellen Sie das kumulative Histogramm vor und nach dem Histogramm-Ausgleich dar. Entspricht das Histogramm Ihren Erwartungen?

Beschreiben Sie in eigenen Worten, was nach Anwendung des Histogramm-Ausgleichs auf Bild copter2.jpg besser und was schlechter geworden ist.
Hätte man eine qualitativ ähnliche Verbesserung auch mit Brigtness/Contrast erhalten können?

Hinweise zur Implementierung:

Mit int[] hist = ip.getHistogram() erhält man das Histogramm als int-Array.
Mit ip.applyTable(hist) wendet man ein Lookup-Table auf das Bild an.
Nachdem das kumulative Histogramm in Array float[] h_arr (mit X-Werten in Array float[] x_arr) berechnet wurde, läßt es sich durch

PlotWindow p1 = new PlotWindow("Titel","x","y",x_arr,h_arr);

p1.setColor(Color.blue);

p1.draw();

anzeigen

A.6. Aufgabe FFT / Sinus Gratings

(a) sinus01 (b) sinus02

Teil A:

Den Teil A.1 machen Sie am besten mit einem Plugin (evtl. sogar mit GUI-Elementen gemäß Ü10).
Die Teile A.2-A.3 gehen über direkte ImageJ-Benutzung, bei A.4 müssen Sie für die Lochblende wieder Ihr Plugin aus A.1 erweitern.

Erzeugen Sie Bilder im Ortsraum, die etwa so aussehen wie oben in (a) und (b) gezeigt (statt des farbigen Randes nehmen Sie einen 5 Pixel breiten Rand mit Grauwert 200). Da die dominante Funktion in diesen synthetischen Bildern der Sinus ist, nennt man sie auch Sinus-Gratings. Der Sinus soll dabei zwischen Grauwert 0=Schwarz und 255=Weiß verlaufen. Die Bildgröße sollte eine 2er-Potenz sein, also z.B. 256x256 oder 512x512. (*)
Installieren Sie das Plugin FFTJ von https://imagej.nih.gov/ij/, (Download & unzip in Plugin-Folder, dann Plugins – Compile and Run – FFTJ), machen Sie damit die FFT dieser Bilder (a) und (b) und visualisieren Sie das (logarithmierte) Power- oder Frequenzspektrum der FFT. Wie Sie sehen werden, ist es nicht ganz einfach, im Powerspektrum etwas zu sehen. Probieren Sie daher verschiedene Visualisierungsformen aus

o Frequenz-Ursprung in Ecke oder in Mitte,

o logarithmiert vs. unlogarithmiert,

o Plots von geeigneten Schnittlinien (Line Selection Tool, dann Analyze – Plot Profile = Strg-K), wenn man dann den Profilplot auf „Live“ stellt, kann man das Profil verschieben und den Effekt im Profilplot direkt sehen),

o Colormaps = Lookup Tables und/oder Brightness Adjust,

Wie lassen sich im Ergebnis die wesentlichen Eigenschaften des FFT-Bildes beschreiben? Erklärung?

Wie ändert sich das FFT-Ergebnis, wenn man den 5 Pixel breiten Rand weglässt?
Wie ändert sich das FFT-Ergebnis, wenn man im Sinus-Grating ausserhalb einer Lochblende von z.B. 100 Pixeln Durchmesser alles auf einen mittleren Grauwert setzt? Wählen Sie für diesen Aufgabenteil ein Sinus-Grating mit 50 Wellen (statt 10).
Wie hängt das Resultat im Frequenzraum von der Größe der Lochblende im Ortsraum ab?
In einem Profilplot des Frequenzspektrums werden Sie Oszillationen entdecken. Können Sie erklären, wodurch diese verursacht werden?

Teil B:

Gehen Sie nun den umgekehrten Weg und starten Sie mit zwei kleinen runden Scheiben im Frequenzraum. Können Sie die Scheiben so anordnen, dass nach inverser FFT das Bild im Ortsraum reell ist? Welches Bild erhalten Sie, wie ändert es sich mit Lage und Radius der Scheiben? Erklärung?
Ersetzen Sie die Scheiben durch Gaussglocken vergleichbarer Breite. Wie ändert sich das Bild im Ortsraum (nach inverser FFT)? Die so erhaltenen Filter gehören zur Funktionenklasse der Gabor-Wavelets. Sie spielen eine große Rolle in Modellen zur visuellen Wahrnehmung bei Mensch und Tier.

In [Lad+93] werden diese Gabor-Wavelets weitergehend beschrieben und als Feature-Basis für die Gesichtserkennung eingesetzt.

(*) Warum? - Die meisten FFTs sind für 2er-Potenzen viel performanter als für Bildlängen 255 oder 260 oder sonstige Werte.

Alternativ könnte man statt des FFTJ Plugins auch die in ImageJ eingebaute Funktionalität „Process – FFT“ verwenden, die die Fast Hartley Transform (FHT) benutzt. Diese scheint aber anders definiert zu sein, es kommen andere FFT-Bilder heraus. Es wird daher empfohlen, FFTJ zu benutzen.

Literatur

· [Lad+93] M. Lades et al.: Distortion invariant object recognition in the dynamic link architecture, IEEE Transaction on Computers, 42, 1993, p. 300-311. (PDF)

A.7. Aufgaben Bildrestauration

Frequenz-Störung

Jet-frequency Jet-filtered

Gegeben das Bild links Jet-frequency.jpg mit einer starken Frequenz-Störung.

Entwickeln Sie einen geeigneten Filter, mit dem sich die Störung möglichst weit beseitigen läßt, zum Beispiel wie im Bild rechts.

Hinweise zu ImageJ / Plugin FFTJ:

· Um die Berechnungen schnell ausführen zu können, empfiehlt es sich, aus Jet-frequency.jpg einen 256x256-Ausschnitt zu nehmen.

· Wie man die Methoden aus FFTJ in seinem eigenen Plugin-Java-Code ansprechen kann, ist in TR_IJ_FFT.pdf beschrieben. Die dort erläuterte Beispieldatei Ideal_LP_FFTJ.java kann aus dem Ordner images/ geladen werden und muss im Ordner plugins/FFTJ installiert werden.

Unsharp-Masking

Das Bild building-1.jpg enthält ein unscharfes Bild (Das scharfe Original steht in building-sw.jpg). Implementieren Sie die Methode des Unsharp-Masking und erzeugen Sie damit eine geschärfte Version des Bildes.

Experimentieren Sie mit anders unscharf gemachten Bildern des Originals building-sw.jpg. Können Sie Aussagen darüber machen, bei welchen Parametern (sigma, alpha) man die besten Resultate erhält? Welche Artefakte beobachten Sie in den geschärften Bildern?

Etwas detaillierter:

· Sie können das künstlich unscharf gemachte Bild building-1.jpg auch selbst erzeugen, indem Sie einen Gaussian Blur auf building-sw.jpg anwenden (dann haben Sie die Unschärfe in der Hand).

· Schreiben Sie ein Makro, das eine Funktion enthält, die das Unsharp-Masking realisiert.

· Rufen Sie im Makro diese Funktion für verschiedene -Werte auf erzeugen Sie so eine ganze Bildserie.

· Packen Sie alle Bilder (Original, künstlich unscharfes Bild und die geschärfte Bildserie) in einen ImageStack („Convert to Stack“), dann können Sie die Bilder im Stack mit „<“ und „>“ besser vergleichen.

A.8. Aufgabe Warping

right warp_out

Implementieren Sie eine Warping-Routine, die folgendes leistet:

Das Input-Bild (z.B. right.jpg) wird angezeigt und der User clickt 4 Positionen an, die für die neue Lage der Bildecken stehen.
Sodann wird aus dem Raum der Euklid-Transformationen (Aspect Ratio bleibt erhalten!) diejenige gesucht, die am besten zu den neuen Ecken paßt. (Hinweis: s. Folie zu Schritt 2a des Warping-Algorithmus)
Mit dieser Transformation wird das Input-Bild gewarpt (Euclidean Warp) und in einem Zielbild gezeigt, das die gleichen Abmessungen hat wie das Input-Bild. "Leere" Pixel sollen auf Blau gesetzt werden.

Hinweise:

Das Anclicken der 4 Positionen macht man am besten mit dem Polygon-Selection-Tool. Die polygonale ROI kann man in Java mit PolygonRoi poRoi = imp.getRoi() abfragen (Doku zu Klasse PolygonRoi lesen, imp = ImagePlus-Objekt)
Zum Matrix-Lösen greift man am beste auf ein Matrix-Package wie Jama (http://math.nist.gov/javanumerics/jama/) zurück. Jama bietet Matrix-Funktionen unter Java, z.B. Matrix A.solve(Matrix B), was die Lösung X des Gleichungssystems A*X = B ermittelt, auch im Least-Square-Sinne.
Jama-Installation: Jama-1.0.2.zip (Version mit Sourcen) herunterladen, entpacken ins Verzeichnis, das das eigene Plugin enthält, dann alle .class-Files löschen (damit erzwingen wir Re-Compile, denn die .class-Files aus dem Download funktionieren nicht mit ImageJ's JRE). Dann eigenes Plugin compilieren.

A.9. "Kleiner ist nicht immer feiner"

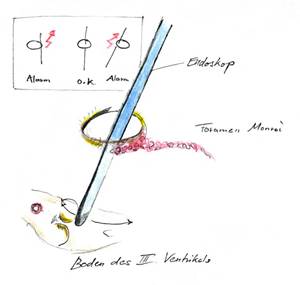
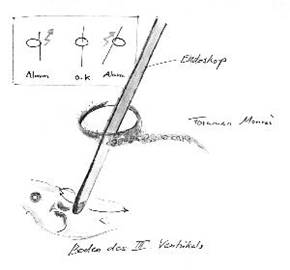
zeichnung01s zeichnung-bil-blank

Das gezeigte linke Bild zeichnung01.jpg hat eine Auflösung von 1423x1499.

(Das Bild zeigt eine Skizze zu einer neuroendoskopischen OP-Technik, bei der auch Bildverarbeitung zum Einsatz kommt. Die Zusammenhänge sind allerdings hier ohne Belang, das Bild wurde nur gewählt, weil die Zeichnungselemente (dünne Linien) besonders deutlich zeigen, wenn beim Verkleinern etwas schief läuft.)

Ziel: Wie erzeugt man von diesem Bild eine qualitativ möglichst hochwertige Verkleinerung auf 20% der Originalgröße? Ein erster Ansatz könnte darin bestehen, einfach nur jede 5. Linie aus dem Originalbild zu nehmen. Das Ergebnis wir ähnlich wie das rechte Bild zeichnung-bil-blank.jpg aussehen, also wenig befriedigend sein (Linien sind unterbrochen oder in Stufen zerhackt, Schrift schlecht lesbar, "körniger" Eindruck).

Aufgaben:

Implementieren Sie mittels der Warping-Verfahren eine eigene Resize-Routine (oder nutzen Sie die "Image - Resize"-Möglichkeiten von ImageJ in Ihrem Plugin) mit den Optionen 'bilinear' und 'nearest neighbour'.
Egal ob 'bilinear' oder 'nearest neighbour', dasResultat wird wahrscheinlich weiterhin so schlecht wie das rechte Bild aussehen, wesentlich schlechter sein als eine Ver-kleinerung in MATLAB oder Photoshop. Wieso ist das so?

Was muss man also darüber hinaus tun, um eine gute Verkleinerung zu erhalten?

Zusatzaufgabe:

Transformieren Sie zunächst das RGB-Bild auf ein Grauwertbild.

Probieren Sie, ob Sie einen "idealen" Tiefpassfilter, der alle Frequenzen größer als die halbe Maximalfrequenz perfekt unterdrückt, auf das Grauwertbild anwenden können. Welche Artefakte zeigen sich?