Spiele, Simulation und dynamische Systeme

Sinn und Zweck der Simulation

Warum simulieren wir? Fragen nach Sinn und Zweck unserer Handlungen stellt man am besten dem Verhaltensforscher. Er meint: "Angetrieben von seiner Neugier setzt sich der Mensch von frühester Kindheit an aktiv mit seiner Umwelt auseinander; er sucht nach neuen Situationen, um daraus zu lernen. Er manipuliert die Gegenstände seiner Umwelt auf vielerlei Art, und seine Neugier endet erst, wenn ihm das Objekt oder die Situation vertraut wird oder wenn er die Aufgabe, die sich ihm stellte, gelöst hat" (Eibl-Eibesfeldt, 1984).

Warum spielen wir?

· Spielen trainiert Anforderungen, die heute real noch nicht auftreten >> Investition in die Zukunft

· Rollenverhalten >> Spielen hat viel mit Simulation zu tun

Für den Menschen geht es stets darum, das Verhalten der Systeme und Prozesse seiner Umwelt kennenzulernen, um ihre Reaktionen vorhersagen zu können. Das ist ganz natürliches Neugierverhalten. Er will in der Welt besser zurechtkommen. Außerdem will er Systeme bauen, die ihm das Leben erleichtern.

Das klassische Verfahren zur Informationsgewinnung ist das Experiment mit dem zu erforschenden System: Will ich wissen, ob das Hemd passt, ziehe ich es probeweise an.

Experimente mit dem realen Objekt sind nicht immer durchführbar: Versuchsobjekte können unzugänglich sein (zu groß und zu weit weg wie die Planeten - oder auch zu klein wie die Moleküle); die Dauer der Experimente übersteigt manchmal unsere Geduld oder gar unsere Lebensdauer (bei Evolutionsprozessen beispielsweise); manches (wie ein elektrischer Vorgang) geht einfach zu schnell; der Versuch kann zu gefährlich sein (wie das in der Chemie und in der Kerntechnik der Fall ist); mit dem Wetter oder einer Volkswirtschaft zu experimentieren, verbietet sich von selbst.

Einen Ausweg bietet das Experimentieren mit einem Modell. Und genau das nennen wir Simulation. Dabei spielt es zunächst keine Rolle, aus welchem Material die Modelle sind.
AKTIVIERUNG:
a) Aus welchem Material können Modelle sein?
b) Welche Vorteile bieten Modelle?

Sie können ...

... aus Pappe, Holz, Blech und manch anderem Material sein;
... auf dem Papier in Form von Zeichnungen und Berechnungen vorliegen;
... im Computer als Programm existieren;
... in unserem Kopf vorhanden sein (s.u., fallende Leiter).

Vorteile von Modellen

· (meist) billiger als reales System

· zeitlich raffbar oder dehnbar

· Systemzerstörung im Modell gefahrlos und ohne Folgekosten

· gezielte Veränderungen möglich

Modellbildung verursacht aber auch Schwierigkeiten (nach [Bossel94]):

· Modellbildung = (?) schwierige mathematische Konzepte

Konsequenzen:

· man überlässt das Gebiet Spezialisten und verlässt sich auf sie;

· man verweigert die komplexe Analyse, verlässt sich auf einfache, meist falsche Erklärungen.

Beide Wege sind kaum verantwortbar, wenn man später in verantwortlicher Position Entscheidungen treffen muss (z.B. Themen wie CO₂-Dynamik, Aids, Bevölkerungsexplosion, Rezession, Umweltübernutzung und Zusammenbruch u.a.m.)

Was gebraucht wird, ist Verständnis für Dynamische Systeme, insbesondere rückgekoppelte Systeme (aktuelle Zustand von Teil X wirkt maßgeblich auf den Folgezustand anderer Teile, diese wiederum auf andere und damit schließlich in komplexer Weise auf das gesamte System)
AKTIVIERUNG:
Wo begegnen uns rückgekoppelte dynamische Systeme im Alltag?

(Antworten im Leonardo-Beitrag)

Exkurs: Bundestagswahl 2005 als rückgekoppeltes System

ODER Exkurs: Leonardo, WDR5, 30.03.2009, Komplexe Systeme (mp3, 6 min à auch in ILIAS hinterlegt)

Manko unseres Ausbildungssystems: die Fächer Systemwissenschaft, Modellbildung, Dynamische Systeme sucht man in den Curricula bislang noch (fast) vergeblich. Sie gehören aber eigentlich in (fast) jeden Studiengang.

Wir werden versuchen, die Simulation möglichst einfach und praktisch erfahrbar machen. Wir werden auch Mathematik benutzen, aber sie durch Simulationsexperimente so plastisch wie möglich machen.

Wir werden Berechnungsexperimenten mit dem Computer machen. So etwas wird Digitale Simulation genannt.

Wozu ist Simulation gut?

AKTIVIERUNG:
Wo kommt im realen Leben Simulation vor? Welche Berufsgruppen nutzen Simulationen und wollen was mit ihr erreichen?

Dem Wissenschaftler geht es vor allem um das Überprüfen von Theorien: Er baut ein Modell nach den Vorgaben der Theorie und untersucht, ob die Vorhersagen des Modells mit der Wirklichkeit zusammenpassen.
Der Betriebswirtschaftler hingegen sucht nach optimalen unternehmerischen Entscheidungen durch experimentelles Durchspielen von Alternativen.
Der Ingenieur benötigt Unterstützung beim Entwurf und der Optimierung technischer Systeme.
Weitere Simulationszwecke sind: die Wettervorhersage, Prognosen zur Umweltentwicklung, Computer-based Training (CBT; z.B.: ICE-, Kraftwerks-, Flugsimulator).

Wer durch Simulation lernen will, hält sich an die negative Methode

Simulation kann nicht nur darin bestehen, ein Modell zu programmieren, den Computer mit ein paar Daten zu füttern, und sich über die schönen Bilder zu freuen, die der Computer daraufhin liefert.

Denn: Es kann sein,

· dass die Theorie nicht korrekt ins Programm übertragen wurde,

· dass die Theorie nicht wirklich richtig ist.

Die größte Vorsicht ist geboten. Vor allem sollten wir nie Experimente mit dem Computer durchführen, wenn wir von den Resultaten noch gar keine Ahnung haben. Wir verspielen so die Chance, den Unsinn zu bemerken.

Die Gefahr, dass uns der Computer fehlleitet, lässt sich verringern. Grundsätzlich wird man die Experimente planen. Noch vor der Durchführung wird eine - vielleicht zunächst nur grobe - Erwartung hinsichtlich des Ergebnisses gebildet und festgehalten. Also: Erst Erwartung notieren, dann Versuch durchführen.

Ein von der Erwartung abweichendes Simulationsergebnis sollte uns freuen, denn in genau diesem Fall können wir etwas hinzulernen. Man spricht von der negativen Methode, weil Theorie (unsere Erwartung) und Simulationsergebnis entgegengesetzt sind.

Das Hinzulernen gelingt aber nur, wenn wir die Abweichung genau untersuchen und ihrer Ursache nachgehen. Zunächst ist zu prüfen, ob die Abweichung auf einen Programmierfehler oder etwas Ähnliches zurückgeht. Ist das ausgeschlossen, kann es an unserem schlechten Verständnis des simulierten Gegenstands liegen. Eine Fehleranalyse zeigt uns, wo wir falsch liegen und wie wir zu besseren Prognosen kommen können.

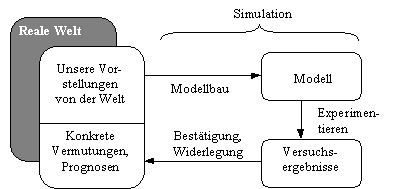
Simulation zur Erkenntnisgewinnung

Da wir nicht Bestätigung suchen, sondern uns über entdeckte Fehler freuen, spricht man (mit Karl Raimund Popper) auch von der negativen Methode. Das ist die Methode der Wissenschaft.

„Simulation im Kopf“

Ein Beispiel: Das Halbkreis-Problem

Aufgabe:

1. Platziere zufällig drei Punkte auf einem Kreis.

2. Wie groß ist die Wahrscheinlichkeit, dass man nun einen Halbkreis auf dem Kreis positionieren kann, so dass er alle drei Punkte überdeckt?

Wir versuchen zuerst, die Frage aus unseren Vorstellungen (‚Simulation im Kopf‘) heraus rein intuitiv zu beantworten. Oder wir „skribbeln“ ein paar Beispiele auf’s Papier, um daraus eine Einschätzung zu gewinnen.

Also: Wie groß ist P? 10%, 25%, 50%, 75%, 90%, 100%?

Eine Simulation am Computer (Processing) nähert sich der Lösung langsam an.

Die Lösung lässt sich auch durch geometrisch-logische Analyse exakt gewinnen.

Durch Vergleich mit der intuitiven Schätzung – die meist anders liegt! – können wir unsere Vorstellungen korrigieren. Diese Erkenntnis verbessert unsere Fähigkeit der intuitiven Schätzung und wir kommen vielleicht der Ursache unserer Fehlschätzung nahe.

Zweites Beispiel: Die fallende Leiter

Ein weiteres Beispiel zeigt den Nutzen, aber auch die Tücken der "Simulation in unserem Kopf":

Aufgabe: Eine Leiter steht zunächst senkrecht an der Wand und rutscht dann langsam mit ihrem Fußpunkt von der Wand weg, wobei der obere Endpunkt der Leiter stets mit der Wand in Kontakt bleibt. Welche Kurve im Raum beschreibt der Mittelpunkt der Leiter? Ist die Kurve eher konkav (nach unten gekrümmt) oder konvex (nach oben gekrümmt)?

Notieren Sie Ihre Erwartung als Skizze auf einem Blatt Papier oder Tablet!

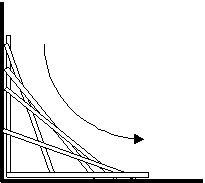
LeiterBild

Die Lösung zeigt sehr schön, dass man auch gegenüber der "Simulation im Kopf", die wir unweigerlich durchführen, wenn wir die Aufgabe zu lösen versuchen, auch eine gewisse Skepsis haben muss, auf dass man sich nicht von falschen (u. U. prägnanten) Denkvorstellungen in die Irre führen läßt.

Fazit

Wir lernen genau dann etwas dazu, wenn die Simulation uns überrascht! Das geht aber nur, wenn wir vorher unsere Erwartungen notiert haben (je genauer, desto beseer, desto mehr können wir lernen). Dann kann uns die Simulation gegenüber diesen Erwartungen eine andere Lösung aufzeigen. Wenn die Simulation uns überraschen kann, falsifiziert sie unsere „Theorie“, d. h. unsere Erwartung, sie zeigt uns, wo unsere Theorie der Welt nicht richtig ist (negative Methode). Wir können dann überlegen, wieso wir zu dieser Fehleinschätzung kamen und können möglicherweise unsere Intuition zur Beurteilung Dynamischer Systeme verbessern. Das ist die Methode der Wissenschaft (Karl Popper, Wissenschaftstheorie, Falsifizierbarkeit von Theorien).

Zurück zur Gliederung